Block Diagrams

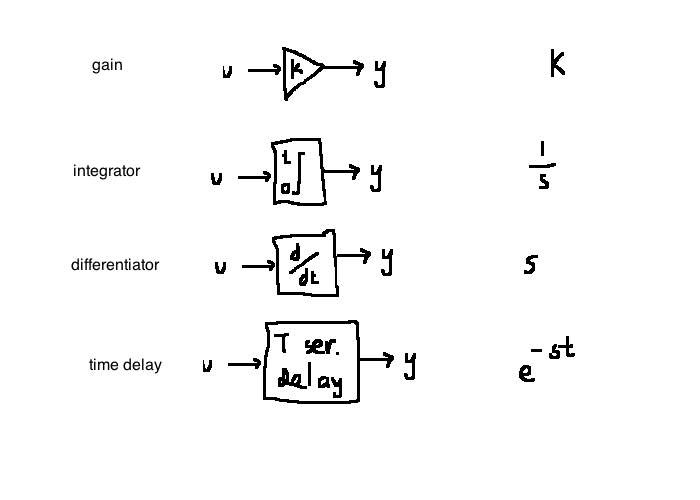
Let \(\mathbb{R}(s)\) be the set of all real rational transfer functions.

• \(G(s) \in \mathbb{R}(s)\) is proper if the degree of the denominator is greater than or equal to the numerator
• Is is strictly proper if it is strictly greater

A complex number \(x \in \mathbb{C}\) is a zero of \(G(s)\) if \(\lim_{s \rightarrow x} |G(s)| = 0\).

• Poles of \(G\) are roots of the denominator

• Zeroes are roots of the numerator

• The transfer function obtained from a state space model is always rational and always proper

e.g. Linearized pendulum

\[\begin{align} \bar{x} &= \begin{bmatrix}\pi\\0\end{bmatrix}, \quad \bar{u}=0\\ \\ \partial \dot{x} &= \begin{bmatrix} 0 & 1 \\ \frac{3g}{l} & 0 \end{bmatrix} \partial x + \begin{bmatrix}0 \\ \frac{3}{Ml^2}\end{bmatrix} \partial u\\ \partial y &= \begin{bmatrix}1 & 0\end{bmatrix} \partial x\\ \\ G(s) &= C(sI-A)^{-1}B + D, \quad (sI-A)^{-1} = \frac{\text{adj}(sI-A)}{\det(sI-A)}\\ &= \begin{bmatrix}1 & 0\end{bmatrix}\begin{bmatrix}s & -1 \\ \frac{-3g}{l} & s\end{bmatrix}^{-1}\begin{bmatrix}0 \\ \frac{3}{Ml^2}\end{bmatrix}\\ &= \begin{bmatrix}1 & 0\end{bmatrix}\begin{bmatrix}s & \frac{-3g}{l} \\ 1 & s\end{bmatrix}^T\begin{bmatrix}0 \\ \frac{3}{Ml^2}\end{bmatrix}\\ &= \frac{\frac{s}{Ml^2}}{s^2 - \frac{3g}{l}}\\ \end{align}\]

Block diagram manipulations

          +------+
  U(s) -->| G(s) |--> Y(s)      Y(s) = G(s)U(s)
          +------+

           +------+
        +->| G(s) |--+
        |  +------+  |
  U(s) -+            +--> Y(s)   Y(s) = (G(s) + H(s))U(s)
        |  +------+  |
        +->| H(s) |--+
           +------+

                                        D(s) 
                                         |
                                         v
                                      +-----+
                  D(s)                | 1/G |
                    |                 +-----+   
          +------+  v                     |   +------+
  U(s) -->| G(s) |--o--> Y(s)   =  U(s) --o-->| G(s) |   Y(s) = D(s) + G(s)U(s)
          +------+                            +------+


             +------+
  U(s) --o-->| G(s) |--+--> Y(s)      Y(s) = G(s)U(s)/(1 + G(s)H(s))
         ^-  +------+  |
         |             |
         |   +------+  |
         +---| H(s) |--+
             +------+ 

Systematic method of finding transfer functions

1. Introduce new variables \(\{v_1, v_2, ... \}\) at the output of every summer
2. Write expressions for inputs of summers in terms of \(\{u, y, v_1, v_2, ...\}\)
3. Write equations for each summer and \(y\)
4. Eliminate \(\{v_1, v_2, ...\}\) from equations

e.g.

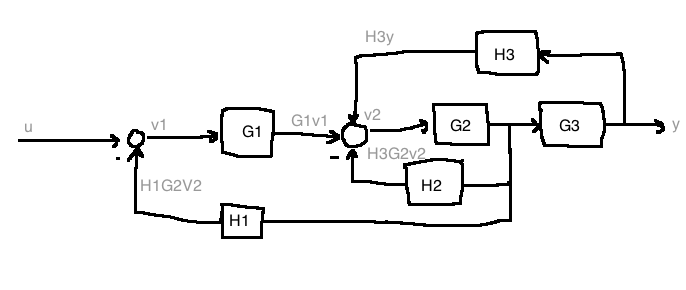
\[\begin{align} y&=G_3G_2v_2\\ v_2 &= H_2y+G_1v_1-H_2G_2v_1\\ v_1&=u-H_1G_2v_2\\ \\ \begin{bmatrix}1 & H_1 G_2 & 0 \\ -G_1 & 1+H_2G_2 & -H_3 \\ 0 & -G_3G_2 & 1\end{bmatrix} \begin{bmatrix}v_1 \\ v_2 \\ y\end{bmatrix} &= \begin{bmatrix}u \\ 0 \\ 0\end{bmatrix}\\ \\ \text{By cramer's rule:}\\ Y(s) &- \frac{ \det\begin{bmatrix}1 & H_1G_2 & u \\ -G_1 & 1+H_2G_2 & 0 \\ 0 & -G_2G_3 & 0\end{bmatrix} }{ \det\begin{bmatrix}1 & H_1G_2 & 0 \\ -G_1 & 1+H_2G_2 & -H_3 \\ 0 & -G_3G_2 & 1\end{bmatrix} }\\ &= \frac{G_1 G_2 G_3}{1 + H_1 H_2 G_2 - H_3 G_3 G_2 + G_1 H_1 G_2} U(s)\\ \end{align}\]